⑤ 円と相似

円と相似

スタートを押して、『円と相似』の問題に取り組んでみよう

問題

円⑤円と相似

中学３年

６章　円

⑤円と相似

1 / 3

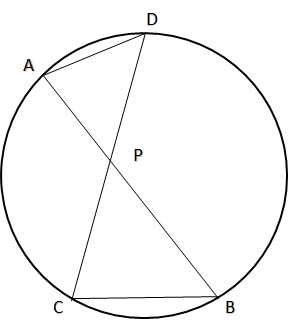
図のように、円の内部の点Pを通る２直線があり、それぞれ円と点A、B、および、C、Dで交わっています。このとき、PA：PC＝PD：PBという関係が成り立つことを証明しなさい。

△APDと△CPBにおいて

弧DBの　ア　は等しいので

∠DAP=∠BCP…①

イ　は等しいので

∠DPA＝∠BPC…②

①、②より

ウ　ので

△APD∽△CPB

相似な図形の対応する辺の比は等しいので

PA：PC＝PD：PB

ア　同位角

ア　錯角

ア　円周角

ア　対頂角

2 / 3

△APDと△CPBにおいて

弧DBの　ア　は等しいので

∠DAP=∠BCP…①

イ　は等しいので

∠DPA＝∠BPC…②

①、②より

ウ　ので

△APD∽△CPB

相似な図形の対応する辺の比は等しいので

PA：PC＝PD：PB

イ　同位角

イ　円周角

イ　対頂角

イ　錯角

3 / 3

△APDと△CPBにおいて

弧DBの　ア　は等しいので

∠DAP=∠BCP…①

イ　は等しいので

∠DPA＝∠BPC…②

①、②より

ウ　ので

△APD∽△CPB

相似な図形の対応する辺の比は等しいので

PA：PC＝PD：PB

ウ　２組の角がそれぞれ等しい

ウ　１辺とその両端の角がそれぞれ等しい

ウ　３組の辺の比がそれぞれ等しい

ウ　２組の辺の比とその間の角がそれぞれ等しい

採点しています

Your score is

The average score is 83%

④円の接線　へ

問題

解答

●●●

『円周角⑤円と相似』の

トリガー　　⇒　　ターゲット

辺の比が等しいことを証明する　　⇒　　 ●●●

三角形の相似条件　　⇒　　 ●●● 　

円がある　　⇒　　 ●●● 　

円周角　　⇒　　 ●●● 　

　　　　　⇒　　 ●●● 　

間違えたり、解らなかったりしたら下の簡単授業動画を見よう。
考え方・やり方に意識を向けてその言葉や流れを覚えよう。

円と相似　まとめダウンロード

わからないときは、解説ページで聞いてみよう

ミスをしたら、失敗学にのせておこう