スポンサーリンク
⑤ 直角三角形の合同条件

直角三角形の合同条件

スタートを押して、『直角三角形の合同条件』の問題に取り組んでみよう
問題
問題
図のように、OA、OB上にOC=ODとなる点C、Dをそれぞれとり、Cを通りOAに垂直な直線と、Dを通りOBに垂直な直線との交点をPとします。このとき、∠POC=∠PODであることを証明しなさい。
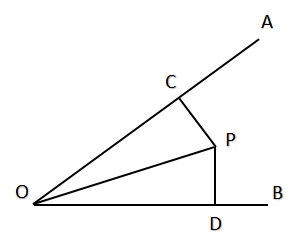
解答
●●●
『三角形と四角形⑤直角三角形の合同条件』の
トリガー ⇒ ターゲット
証明問題 ⇒ ●●●
三角形の合同条件 ⇒ ●●●
自分で大きさが同じと見つけるところ(基本) ⇒ ●●●
図形の問題 ⇒ ●●●
角度を表す ⇒ ●●●
直角三角形の合同条件 ⇒ ●●●
⇒ ●●●
間違えたり、解らなかったりしたら下の簡単授業動画を見よう。
考え方・やり方に意識を向けてその言葉や流れを覚えよう。